| В
этом разделе мы попробуем разобраться с законами Солнечной системы.
Закон всемирного тяготения
Первый закон Кеплера
Возмущения
Второй закон Кеплера
Третий закон Кеплера
Обобщенный третий закон
Кеплера
Космические скорости
Обобщение
В Солнечную систему входят
Солнце, девять больших планет, их спутники, тысячи астероидов, миллиарды
комет, бессчетное количество пылинок, льдинок и просто заряженных частиц.
Более подробно читайте здесь 
Закон
всемирного тяготения
Почти все в Солнечной системе
вращается вокруг Солнца. У некоторых планет есть спутники, но и они, совершая
свой путь вокруг планеты, вместе с нею движутся вокруг Солнца. Солнце обладает
массой, превосходящую массу всего прочего населения Солнечной системы в
750 раз. Благодаря этому Солнце заставляет планеты и все остальное
двигаться по орбитам вокруг себя. В космических масштабах масса является
главной характеристикой тел, потому что все небесные тела подчиняются закону
всемирного тяготения.
По этому закону, открытому
английским физиком Исааком Ньютоном во второй половине 17-го
века, все тела, обладающие массой, притягиваются силой, пропорциональной
произведению их масс и обратно пропорциональной квадрату расстояния между
ними. Такое взаимодействие называют гравитационным, а силу √ гравитацией.
Если
Вы хоть немного знакомы с физикой, Вас не утомит математическая формула
закона:

Здесь F
√ сила притяжения,
m1
и
m2
√
массы двух тел,
R
√ расстояние между ними, G
√ так называемая
гравитационная
постоянная. Ее значение
равно силе, с которой притягиваются
два тела массами по 1 кг,
разнесенные на расстояние 1 м. Эта сила невелика,
именно
поэтому значение гравитационной постоянной,
возможно,
покажется Вам
маленьким:
6,6720.10-11
Н.м2/кг2.
Определить
гравитационную постоянную на опыте с малыми телами впервые удалось Генри
Кавендишу в 1788-м году. Он изучал взаимодействие свинцовых
шаров диаметром 5 и 20 см.
Мы не замечаем того, что,
скажем, два человека гравитационно притягиваются между собою. Если
люди и тянутся друг к другу, то физикой этого не объяснить. Однако опыты
по определению силы, с которой притягиваются
подвешенный
отвесно груз и огромная скала провести вполне возможно. Гравитация
√
сила, которая становится заметной для больших масс.
Не впадите в еще одно распространенное
заблуждение, которое заключается в утверждении, что при взаимодействии
двух тел разных масс более тяжелое действует на легкое тело с большей силой,
чем легкое действует на тяжелое. Это
неверно. Силы, с которыми действуют друг на друга два тела,
одинаковы. Посмотрите на формулу. В любом случае массы тел перемножаются.
Но Вы спросите, отчего же
тогда планетам не вращаться вместе с Солнцем, скажем, вокруг Земли, ведь
сила, с которой действует Земля на
Солнце, равна силе, с которой Солнце
действует на Землю. Это так, силы равны. Но действие этих сил различно.
Пните ногой мяч. А потом с той же силой ударьте по бетонному блоку. Как
говорится, почувствуйте разницу. Одной и той же силы достаточно для того,
чтобы сдвинуть Землю, но ее же не хватит
для того, чтобы заметно побеспокоить
Солнце.
Массы у них разные. Когда камень
падает на Землю, он подчиняется закону всемирного тяготения. Он тоже действует
на
Землю, но ее движение навстречу камню ничтожно мало. Поэтому
мы говорим, что камень падает на Землю.
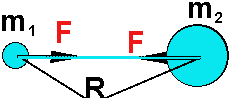 Теперь
остановимся на том, в каком направлении действует сила гравитации. Эта
сила прилагается к одному из взаимодействующих тел и направлена в сторону
другого. К этому другому приложена такая же по величине сила,
но она направлена в сторону первого. Силы направлены
по прямой линии, соединяющей взаимодействующие тела. А если
так, тогда отчего же всё в Солнечной системе
не падает на Солнце? Теперь
остановимся на том, в каком направлении действует сила гравитации. Эта
сила прилагается к одному из взаимодействующих тел и направлена в сторону
другого. К этому другому приложена такая же по величине сила,
но она направлена в сторону первого. Силы направлены
по прямой линии, соединяющей взаимодействующие тела. А если
так, тогда отчего же всё в Солнечной системе
не падает на Солнце?
Всё обязательно попадало
бы на Солнце, если бы это всё стояло на месте. Действующая сила пытается
изменить скорость тела, стремясь ее развернуть по направлению силы. Бросая
камень, мы заметим, что тот не падает
у наших ног, а описывает в воздухе кривую линию.  Сила
притяжения постепенно изменила направление и величину скорости камня,
и тот упал на некотором расстоянии от нас. Чем большую скорость мы сообщим
камню, бросая его, тем дольше придется гравитации менять направление скорости,
тем дальше от нас камень ударится о Землю. А теперь вспомним про
то, что Земля не плоская, а
круглая. Что если мы с такой силой бросим камень, что за каждую секунду
гравитация будет приближать его к Земле на такое же расстояние, на какое
кривая поверхность Земли будет уходить от камня?
В таком случае камень будет двигаться по окружности вокруг Земли, не падая
на нее. Это движение будет происходить под действием силы гравитационного
притяжения. Камень будет пытаться лететь в сторону от Земли, а гравитация
с таким же усердием будет стремиться искривить путь камня в сторону поверхности.
К такому заключению, в частности, пришел И. Ньютон
в своем мысленном бросании камней с высокой горы. Итак,
Солнце
искривляет движение планет, не давая
им разлететься во все стороны. Сила
притяжения постепенно изменила направление и величину скорости камня,
и тот упал на некотором расстоянии от нас. Чем большую скорость мы сообщим
камню, бросая его, тем дольше придется гравитации менять направление скорости,
тем дальше от нас камень ударится о Землю. А теперь вспомним про
то, что Земля не плоская, а
круглая. Что если мы с такой силой бросим камень, что за каждую секунду
гравитация будет приближать его к Земле на такое же расстояние, на какое
кривая поверхность Земли будет уходить от камня?
В таком случае камень будет двигаться по окружности вокруг Земли, не падая
на нее. Это движение будет происходить под действием силы гравитационного
притяжения. Камень будет пытаться лететь в сторону от Земли, а гравитация
с таким же усердием будет стремиться искривить путь камня в сторону поверхности.
К такому заключению, в частности, пришел И. Ньютон
в своем мысленном бросании камней с высокой горы. Итак,
Солнце
искривляет движение планет, не давая
им разлететься во все стороны.
Законы Кеплера
1.
Орбиты
планет представляют собою более сложные фигуры, чем окружность. Еще
в конце 16-го века,
в
начале
17-го (то есть до открытия Ньютоном
закона всемирного тяготения)
Иоганн
Кеплер впервые решился пересмотреть причины
движения планет вокруг Солнца, Луны вокруг Земли. Он ошибался в оценке
природы притягивающей силы, но догадывался, что Солнце искажает притяжением
пути планет, которые стремятся двигаться по прямой. Кеплер на основе
результатов кропотливых и многолетних наблюдений Тихо Браге за планетой
Марс смог определить форму его орбиты. После
длительных расчетов, ошибок, разочарований, перебора множества вариантов
(математика не давала в то время возможности идти другим путем),
Кеплер
достиг согласования своих результатов и записей о наблюдениях датского
астронома. Орбита оказалась эллипсом. Солнце
Кеплер
расположил в одном из фокусов эллипса. Таким
образом, появился первый эмпирический (то
есть выведенный из наблюдений)
закон
Кеплера:
любая планета движется по орбите в виде эллипса, в одном из фокусов которого
находится Солнце. Падающий на землю после нашего броска камень до
момента падения описывает в воздухе траекторию, являющуюся малой частью
эллипса, в одном из фокусов которого находится центр Земли.
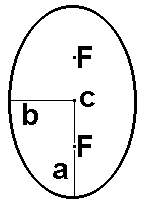 Эллипс
- геометрическая фигура, свойство которой состоит в том, что сумма расстояний
от любой точки эллипса до двух особых точек, именуемых фокусами эллипса
(F), является величиной постоянной. У эллипса еще выделяют точку
центра (С). Основным же понятием для этой фигуры является эксцентриситет.
Эксцентриситет - параметр, являющийся характеристикой вытянутости эллипса.
Он равен отношению расстояния от центра эллипса до его фокуса к длине большой
полуоси (a) или отношению корня из разности квадратов большой и
малой (b) полуосей к длине большой полуоси: Эллипс
- геометрическая фигура, свойство которой состоит в том, что сумма расстояний
от любой точки эллипса до двух особых точек, именуемых фокусами эллипса
(F), является величиной постоянной. У эллипса еще выделяют точку
центра (С). Основным же понятием для этой фигуры является эксцентриситет.
Эксцентриситет - параметр, являющийся характеристикой вытянутости эллипса.
Он равен отношению расстояния от центра эллипса до его фокуса к длине большой
полуоси (a) или отношению корня из разности квадратов большой и
малой (b) полуосей к длине большой полуоси:
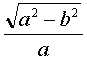
Эксцентриситет обозначается латинской
буквой е. Анализ формул дает нам знать, что для окружности (а=b)
эксцентриситет равен нулю. Другие значения этой величины определяют разомкунтые
кривые. Для параболы (а бесконечно велико) эксцентриситет равен
единице. Эксцентриситет, больший, чем единица, описывает гиперболу.
Надо сказать, что в случае
планет отличие орбит от окружностей невелико (е несильно отличается
от нуля). Значительную вытянутость имеют лишь орбиты Меркурия (е=0,206)
и Плутона (е=0,25). Орбиты астероидов и комет могут иметь различную
вытянутость. Кометные орбиты часто имеют как параболическую, так и гиперболическую
форму. Под гравитационным действием планет кометы иногда искажают свой
путь, ускоряются или замедляются. Результатом этого и может послужить сильное
изменение формы орбиты.
Вспомним
также, что гравитационное взаимодействие присуще всем телам, обладающим
массами. Из-за этого орбиты всех тел Солнечной системы постоянно меняются:
все планеты действуют друг на друга. Такое действие (малое, по сравнению
с действием Солнца) называют возмущающим.
А изменения в пути небесных тел
√
возмущениями.
Например, возмущающая сила гравитационного притяжения Юпитера значительно
меняет орбиты астероидов. Действие на Луну Земли и Солнца делают совершенно
непригодными для расчетов ее орбиты законы Кеплера.
2.
 Изучая
по наблюдениям закономерности движения планет, Кеплер смог открыть
и такое правило: за
любые равные промежутки времени линия, соединяющая Солнце с планетой, покрывает
равные по площади участки внутри эллипса. Это второй
закон Кеплера или закон площадей.
Он предвосхитил собою позднее выведенный
закон
сохранения момента импульса, на котором мы здесь останавливаться не станем.
Следствие из этого закона такое: чем ближе планета к Солнцу, тем быстрее
она движется. Догадываетесь почему? Изучая
по наблюдениям закономерности движения планет, Кеплер смог открыть
и такое правило: за
любые равные промежутки времени линия, соединяющая Солнце с планетой, покрывает
равные по площади участки внутри эллипса. Это второй
закон Кеплера или закон площадей.
Он предвосхитил собою позднее выведенный
закон
сохранения момента импульса, на котором мы здесь останавливаться не станем.
Следствие из этого закона такое: чем ближе планета к Солнцу, тем быстрее
она движется. Догадываетесь почему? 
Интересно, что закон площадей
Кеплер
открыл раньше, чем форму планетных орбит. Справа Вы видите движение
кометы Галлея вокруг Солнца и орбиты планет: Юпитера, Сатурна, Нептуна,
Урана и Плутона.
3.
Наконец,
Кеплер
отметился еще и третьим законом планетных
движений.
Он вычислил, что отношения
кубов больших полуосей
орбит
и квадратов периодов обращения планет вокруг Солнца √
величины равные.
Или
 , ,
где a1
и a2
√
длины больших полуосей
орбит двух планет, а T1
и
T2
√ периоды их обращения вокруг Солнца.
Если,
скажем, мы знаем длину большой полуоси орбиты Земли и период ее движения
вокруг Солнца (год), то, установив
из наблюдений период движения другой планеты, мы легко можем вычислить
большую полуось ее орбиты. Если принять большую полуось Земной орбиту за
единицу, а период обращения измерять в годах, то, используя в качестве
первой планеты в формуле третьего закона Землю, мы сможем переписать закон
так:
a3=T2,
где
а измеряется
в длинах большой полуоси земной орбиты, а Т √
в годах.
Длину
большой полуоси орбиты Земли издавна принято называть астрономической единицей.
Расстояние до других планет в астрономических единицах люди узнали гораздо
раньше, чем расстояние от Земли до Солнца, благодаря третьему закону Кеплера.
Повторим, что законы Кеплера
√
следствие его непревзойденного усердия в математической обработке результатов
наблюдений. Это √ наблюдательные законы.
Они отображают закономерности, но не выявляют причин. После появления закона
всемирного тяготения стало очевидным, что законы Кеплера
√ лишь следствие физического
свойства любых тел, обладающих массами, притягиваться друг другом.
Обобщенный третий закон Кеплера
Законы
Кеплера
верны для описания группы тел, масса
одного их которых во много раз больше массы остальных.
В случае Солнечной системы таким массивным
телом является Солнце. Для того чтобы, скажем, описать движение двух близких
друг к другу звезд, законов Кеплера вообще не достаточно. Ньютон
смог ⌠поправить■ своего предшественника,
выведя третий закон Кеплера для тел, массы
которых надо учитывать. Этот закон называют обобщенным третьим законом
Кеплера.
В него уже входят значения масс:

С помощью этого закона можно
сравнить движение спутника с массой m1
вокруг тела с массой M1
и
движение спутника с массой m2
вокруг
тела
с массой М2.
Если мы ограничимся Солнечной системой, то М1=М2,
ведь это масса Солнца. Массы
всех других тел Солнечной системы малы, по сравнению с массой Солнца, можно
принять их равными нулю, и Ньютонов
закон преобразуется в обычный третий закон Кеплера.
Космические скорости
Ньютон
пошел гораздо дальше Кеплера. Он смог доказать что, при достижении
некоторой скорости тело начинает двигаться вокруг центра вращения не по
эллипсу, а по параболе. Эта скорость всецело зависит от массы центрального
тела и расстояния до него:

Она называется второй
космической
или параболической скоростью.
Для
поверхности Земли эта скорость равна 11,2 км в
секунду.
Если разогнать ракету до такой скорости, она будет двигаться по параболе,
а это уже незамкнутая траектория. Ракета не станет спутником Земли, а навсегда
удалится от нее, став спутником Солнца.
Давайте сделаем шаг назад
от эллипсов, к круговой орбите. Ту
скорость, которая соответствует круговому движению, называют первой
космической скоростью. Она определяется из похожего соотношения:
 Для поверхности Земли первая
космическая или круговая скорость равна
7,9 км в секунду.
Диапазон скоростей между этой величиной и второй космической соответствует
движению тела по эллипсу.
Для поверхности Земли первая
космическая или круговая скорость равна
7,9 км в секунду.
Диапазон скоростей между этой величиной и второй космической соответствует
движению тела по эллипсу.
Наконец, превысив
вторую космическую скорость, мы получаем гиперболическую траекторию движения.
Заметьте,
что в приведенных выше формулах (космические скорости, закон всемирного
тяготения, обобщенный закон Кеплера)
расстояния
отсчитываются от центра небесных тел (Земли,
Солнца), а не от их поверхности.
Поэтому
R
для
поверхности Земли не 0, а примерно 6 400
км.
Для планеты и Солнца существует
и третья космическая скорость. Эта скорость
соответствует параболической скорости по отношению к Солнцу на расстоянии
радиуса планетной орбиты. Она равна примерно 42
км в секунду для Земли.
Если
учесть, что Земля уже несется по орбите, покрывая за секунду 30 км,
то, запуская ракету
в
направлении движения Земли по орбите, нам достаточно придать ей скорость,
превышающую 12 км в секунду, чтобы эта ракета смогла покинуть
Солнечную систему. Впрочем, мы можем
и еще выиграть в скорости, если вспомним, что Земля вращается вокруг оси.
Точки на экваторе нашей планеты движутся наиболее быстро: почти
полкилометра
в секунду. Поэтому, желая совершить наиболее
экономичный запуск ракеты с Земли к
звездам, мы должны были бы расположить
стартовую площадку на экваторе, обеспечить направление запуска по касательной
к поверхности, нацеленной на восток,
и нажать на кнопку пуск в полночь. Попытайтесь сами сначала объяснить
себе, почему именно так, а не иначе, а потом... найти то обстоятельство,
которое мы не учли, и из-за которого все получится совсем не так.
Итак,
мы выяснили, что все движения в Солнечной системе подчиняются закону всемирного
тяготения. Исходя из малой массы планет и тем более прочих тел Солнечной
системы, можно приближенно считать, что движения в околосолнечном пространстве
подчиняются законам Кеплера. Все
тела движутся вокруг Солнца по эллиптическим орбитам, в одном из фокусов
которых находится Солнце. Чем ближе к Солнцу небесное тело, тем быстрее
его скорость движения по орбите (планета
Плутон, самая далекая из известных, движется в 6 раз медленнее Земли).
Тела
могут двигаться и по разомкнутым орбитам: параболе или гиперболе. Это случается
в том случае, если скорость тела равна или превышает значение второй космической
скорости для Солнца на данном удалении от центрального светила. Если речь
идет о спутнике планеты, то и космическую скорость надо рассчитывать относительно
массы планеты и расстояния до ее центра.
Обратитесь к странице о составе
Солнечной системы. Вы узнаете с помощью нее некоторые другие особенности
движения планет и других тел Солнечной системы, которые вовсе не следуют
из описанных выше законов
|


 Теперь
остановимся на том, в каком направлении действует сила гравитации. Эта
сила прилагается к одному из взаимодействующих тел и направлена в сторону
другого. К этому другому приложена такая же по величине сила,
но она направлена в сторону первого. Силы направлены
по прямой линии, соединяющей взаимодействующие тела. А если
так, тогда отчего же всё в Солнечной системе
не падает на Солнце?
Теперь
остановимся на том, в каком направлении действует сила гравитации. Эта
сила прилагается к одному из взаимодействующих тел и направлена в сторону
другого. К этому другому приложена такая же по величине сила,
но она направлена в сторону первого. Силы направлены
по прямой линии, соединяющей взаимодействующие тела. А если
так, тогда отчего же всё в Солнечной системе
не падает на Солнце?
 Сила
притяжения постепенно изменила направление и величину скорости камня,
и тот упал на некотором расстоянии от нас. Чем большую скорость мы сообщим
камню, бросая его, тем дольше придется гравитации менять направление скорости,
тем дальше от нас камень ударится о Землю. А теперь вспомним про
то, что Земля не плоская, а
круглая. Что если мы с такой силой бросим камень, что за каждую секунду
гравитация будет приближать его к Земле на такое же расстояние, на какое
кривая поверхность Земли будет уходить от камня?
В таком случае камень будет двигаться по окружности вокруг Земли, не падая
на нее. Это движение будет происходить под действием силы гравитационного
притяжения. Камень будет пытаться лететь в сторону от Земли, а гравитация
с таким же усердием будет стремиться искривить путь камня в сторону поверхности.
К такому заключению, в частности, пришел И. Ньютон
в своем мысленном бросании камней с высокой горы. Итак,
Солнце
искривляет движение планет, не давая
им разлететься во все стороны.
Сила
притяжения постепенно изменила направление и величину скорости камня,
и тот упал на некотором расстоянии от нас. Чем большую скорость мы сообщим
камню, бросая его, тем дольше придется гравитации менять направление скорости,
тем дальше от нас камень ударится о Землю. А теперь вспомним про
то, что Земля не плоская, а
круглая. Что если мы с такой силой бросим камень, что за каждую секунду
гравитация будет приближать его к Земле на такое же расстояние, на какое
кривая поверхность Земли будет уходить от камня?
В таком случае камень будет двигаться по окружности вокруг Земли, не падая
на нее. Это движение будет происходить под действием силы гравитационного
притяжения. Камень будет пытаться лететь в сторону от Земли, а гравитация
с таким же усердием будет стремиться искривить путь камня в сторону поверхности.
К такому заключению, в частности, пришел И. Ньютон
в своем мысленном бросании камней с высокой горы. Итак,
Солнце
искривляет движение планет, не давая
им разлететься во все стороны.
 Эллипс
- геометрическая фигура, свойство которой состоит в том, что сумма расстояний
от любой точки эллипса до двух особых точек, именуемых фокусами эллипса
(F), является величиной постоянной. У эллипса еще выделяют точку
центра (С). Основным же понятием для этой фигуры является эксцентриситет.
Эксцентриситет - параметр, являющийся характеристикой вытянутости эллипса.
Он равен отношению расстояния от центра эллипса до его фокуса к длине большой
полуоси (a) или отношению корня из разности квадратов большой и
малой (b) полуосей к длине большой полуоси:
Эллипс
- геометрическая фигура, свойство которой состоит в том, что сумма расстояний
от любой точки эллипса до двух особых точек, именуемых фокусами эллипса
(F), является величиной постоянной. У эллипса еще выделяют точку
центра (С). Основным же понятием для этой фигуры является эксцентриситет.
Эксцентриситет - параметр, являющийся характеристикой вытянутости эллипса.
Он равен отношению расстояния от центра эллипса до его фокуса к длине большой
полуоси (a) или отношению корня из разности квадратов большой и
малой (b) полуосей к длине большой полуоси:
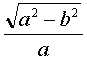
 Изучая
по наблюдениям закономерности движения планет, Кеплер смог открыть
и такое правило: за
любые равные промежутки времени линия, соединяющая Солнце с планетой, покрывает
равные по площади участки внутри эллипса. Это второй
закон Кеплера или закон площадей.
Он предвосхитил собою позднее выведенный
закон
сохранения момента импульса, на котором мы здесь останавливаться не станем.
Следствие из этого закона такое: чем ближе планета к Солнцу, тем быстрее
она движется. Догадываетесь почему?
Изучая
по наблюдениям закономерности движения планет, Кеплер смог открыть
и такое правило: за
любые равные промежутки времени линия, соединяющая Солнце с планетой, покрывает
равные по площади участки внутри эллипса. Это второй
закон Кеплера или закон площадей.
Он предвосхитил собою позднее выведенный
закон
сохранения момента импульса, на котором мы здесь останавливаться не станем.
Следствие из этого закона такое: чем ближе планета к Солнцу, тем быстрее
она движется. Догадываетесь почему? 
