|
||
|
|
||
| Расстояние между объектами в астрономии
√ понятие очень важное. Как Вы увидите в дальнейшем, точное измерение расстояний
позволяет судить ученым не только о километрах, но и о годах, килограммах,
о таких жизненно важных вопросах, как извечное ╚Быть или не быть╩┘
Солнечная система
Астрономическая единицаНачнем с того, что километры астрономов обычно не интересуют. Разве что в окрестностях Солнца. Если написать, что до Луны На практике из наблюдений можно узнать период обращения небесного тела вокруг Солнца. А дальше очень просто из третьего закона Кеплера высчитать длину большой полуоси орбиты небесного тела. РадиолокацияПрямое (ну или почти) измерение расстояний подвластно астрономам на дистанциях в несколько астрономических единиц при помощи радиолокации. Это очень точный способ. Однако, при его использовании необходимо учитывать движение Земли и исследуемого тела, а также знать скорость света. Посланный радиотелескопом сигнал отражается от поверхности небесного тела и снова принимается на Земле. Радиолуч проходит двойное расстояние (туда-обратно), зная время, которое затратил сигнал на преодоление пути, можно высчитать само расстояние. Остается учесть взаимные перемещения тел за время движения сигнала, но это также дело сравнительно нетрудное. Горизонтальный параллакс 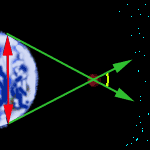 Если
смотреть на один и тот же предмет с разных мест, то он будет менять свое
расположение на фоне более удаленных предметов. Если эти неблизкие предметы
далеки настолько, что их видимым перемещением при перемещении наблюдателя
можно пренебречь, то из геометрических соображений совсем нетрудно
узнать расстояние до близкого предмета. Если
смотреть на один и тот же предмет с разных мест, то он будет менять свое
расположение на фоне более удаленных предметов. Если эти неблизкие предметы
далеки настолько, что их видимым перемещением при перемещении наблюдателя
можно пренебречь, то из геометрических соображений совсем нетрудно
узнать расстояние до близкого предмета.
Для измерения расстояний до объектов внутри Солнечной системы точно отмечают на небе положение этого объекта относительно звезд, которые достаточно удалены. Наблюдения одновременно проводят из двух разнесенных на большое расстояние мест земной поверхности (сотни, тысячи километров). При этом, положение объекта относительно звезд для каждого места наблюдения будет своим. Зная расстояние между точками наблюдения, зная угловое расстояние между положениями объекта для каждой точки, нет ничего проще, чем узнать расстояние до объекта. Такой способ определения расстояний называют методом горизонтального параллакса. Параллакс √ это смещение, то самое смещение объекта на фоне звезд при смене места наблюдения. Размеры тел Солнечной системыОпределенное любым способом расстояние до небесного тела делает простым выяснение его размеров. Для этого кроме самого расстояния нужно знать угловые размеры тела. Чистая геометрия, никакой астрономии. Если тело настолько мало, что угловых размеров выяснить не удается, приходится строить догадки об отражательной способности поверхности тела (альбедо). Тела, находящиеся на одном удалении, с одним и тем же альбедо, но разных размеров, будут сиять тем ярче, чем они больше. Поэтому, примерные размеры малых небесных тел, в основном, астероидов, узнать тоже можно, учитывая расстояния до тел и альбедо их поверхности. Попробуйте осознать число 40700000000000 км. Пока вы считали знаки и
разбивали их на тройки, можно было выпить чаю. Астрономы не любят заниматься
такой работой, как разгребание нулей в астрономических числах. Они сделали
все возможное для того, чтобы эти числа сделать земными. Расстояние до
ближайшей звезды (именно его вы пытались постигнуть) можно примерно записать
Световой год √ это не время. Это расстояние,
проходимое за время. Световой год √ путь, проходимый светом за один год.
Из самых удаленных уголков Вселенной свет до нас добирается более 95 000 000 000 000 000 000 000. Парсек и годичный параллаксСветовой год √ не практическая единица. Из наблюдений расстояния в световых годах не получают. Наблюдательная единица √ парсек (пс). Расстояние до не слишком далеких звезд (десятки световых лет) определяют
с помощью известного нам
Наблюдения будут наиболее продуктивны, если проводить их с промежутком в полгода: Земля перенесется за это время в противоположную точку своей орбиты, и расстояние между пунктами наблюдения будет максимальным. Кроме того, лучше всего выбирать моменты для наблюдений так, чтобы линия, соединяющая точки наблюдения, была перепендикулярна направлению на звезду. Расстояние в один парсек соответствует
смещению звезды на фоне далеких объектов на 1'' при перемещении наблюдателя
на 1 радиус земной орбиты. Парсек √ сокращение слов параллакс и секунда.
Смещение звезд при таких наблюдениях называют Звезды-двойникиДаже орбита Земли мала по сравнению с теми расстояниями, с которыми астрономам приходится работать. Годичный параллакс бессилен для объектов вне крохотной части нашей Галактики поблизости от Солнца. Астрономы нашли еще несколько, способов. Правда, надо отметить, что эти способы уже несравнимы по точности с точностью метода параллакса. Существуют звезды, которые с правильным периодом меняют свои размеры и, следовательно, яркость. Звезды, меняющие свою яркость, называют переменными. Есть несколько типов переменных звезд. Но некоторые из этих разновидностей имеют для измерения расстояний особое значение. Среди тех переменных звезд, расстояние до которых определимы с помощью метода годичного параллакса, выявили тип звезд с очень интересной особенностью. Период колебания их яркости зависит от массы звезды. Массой определяется средняя светимость звезды, поэтому, выявив период колебания блеска, всегда можно узнать и светимость. А раз мы знаем светимость, мы можем сопоставить ее с яркостью звезды на небе и высчитать расстояние.Цефеиды Представьте себе ряд одинаковых фонарей. Если все их погасить, а оставить какой-то один, то Вы сможете по тому, насколько ярко выглядит фонарь, сказать, далеко фонарь или близко. Астрономы обладают точными приборами, поэтому они определяют и то, насколько далеко или близко расположена звезда. Столь полезный тип переменных звезд называют Если бы то, что вынесено в заголовок этого абзаца, имело место, работа криминалистов заметно усложнилась бы. Астрономы, напротив, любят одинаковые признаки, их удобно выявлять на далеких расстояниях. В разделе о звездах сказано, что масса, цвет и яркость всех звезд главной последовательности взаимосвязаны. Это обстоятельство иногда помогает астрономам высчитывать расстояние. Здесь очень важно убедиться в том, что звезда и впрямь принадлежит главной последовательности. Это делается при изучении спектра звезды. Если принадлежность выявлена, то дальше все просто: цвет звезды определяется ее массой, массой определяется светимость. Сопоставляем яркость и светимость и находим расстояние. К сожалению, этот способ весьма грубо определяет искомую нами на этой странице величину.Одинаковые отпечатки пальцев В далеких звездных системах, там, где яркости цефеид не хватает, необходимо найти еще какие-нибудь более яркие объекты, которые вели бы себя одинаково. Таким свойством обладают вспышки сверхновых звезд в двойных системах. Спад их яркости после самой вспышки идет во всех случаях одинаково, так как в двойных системах всегда взрываются звезды одинаковой массы. Одинаковы, конечно, и светимости вспышек. Сверхновая √ объект, сравнимый по яркости с самой галактикой, поэтому их находят очень далеко от Земли. Исследуя то, как сверхновая ведет себя после вспышки, определяют, принадлежит ли взорвавшаяся звезда двойной системе. Если так, то все идет по тому же сценарию. Сравнивают известную светимость с яркостью и находят расстояние. Там, где не видны никакие звезды Всему, видимо, есть предел. На некотором расстоянии от нашей планеты нельзя рассмотреть никаких звезд даже в очень хорошие телескопы. Как определять расстояния до далеких галактик? Нашелся способ и для этого. Связав скорость удаления относительно близких галактик с расстоянием до них, определенным по цефеидам и сверхновым, удалось найти примерное значение коэффициента пропорциональности между этими величинами. Скорость галактик определяют по красному смещению линий в их спектрах.
Согласно эффекту
Доплера, свет от удаляющегося объекта краснеет. По величине этого
покраснения и находят скорость галактики. Сейчас значение коэффициента
пропорциональности между скоростью и расстоянием (постоянная
Хаббла) считается примерно Никакие объекты не могут двигаться быстрее, чем свет. Самое большое расстояние, на которое мы можем заглянуть равно произведению скорости света и возраста Вселенной, так как свет просто не успел дойти из более дальних областей. Так вот взаимосвязаны время и пространство. Итак, давайте выявим способы основные способы определения расстояний. Особняком стоит Солнечная система, в которой действенны радиолокация, законы Кеплера и горизонтальный параллакс. Для далеких небесных тел существует четкая последовательность способов, каждый последующий из которых опирается на предыдущий. Годичный параллакс является основой шкалы расстояний. По нему выявлены закономерности в блеске Цефеид. По цефеидам ╚откалибровали╩ способ определения расстояния по сверхновым. Наконец, сверхновые помогли вычислить постоянную Хаббла. Если на любом из этих шагов допущена неточность, все последующие способы становятся еще более неточными. Над уточнением все соотношений, по которым определяются расстояния, астрономы усиленно работают. Уточнений, пожалуй, не требует годичный параллакс. Но и здесь нет предела увеличению точности наблюдений. Размеры небесных тел определяются на основе
их видимых угловых размеров и найденных расстояний. Размеры звезд находят
из теоретических расчетов, опирающихся на исследование спектра звезды.
Угловые размеры самых больших или очень близких звезд удается сегодня почти
буквально разглядеть с использованием интерферометров.
Интерферометры - связанно работающие телескопы.
Сигнал от двух и более телескопов поступает в один центр и складывается
там. За счет этого такая система может "видеть" детали столь малые по размерам,
что рассмотерть их мог бы одиночный телескоп с диаметром объектива равным
расстоянию между использующимися телескопами. Метод интерферометров требует
очень точного согласования в работе всех применяемых инструментов. Отклонения,
допустимые в такой системе сравнимы с длиной световой волны. Самым большим
оптическим интерферометром сейчас является блок из четырех восьмиметровых
(по диаметру объектива) телескопов VLT
(Very Large Telescope - Очень Большой Телескоп).
|
||
|
|


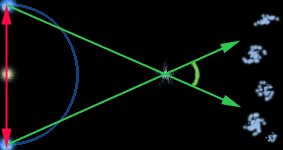 Перемещение
наблюдателя по поверхности ограничено скромными по космическим меркам размерами
нашего голубого шарика. Для звезд эти размеры до смешного малы. Поэтому,
чтобы увидеть перемещение звезд на фоне галактик, наблюдения производят
из разных точек земной
Перемещение
наблюдателя по поверхности ограничено скромными по космическим меркам размерами
нашего голубого шарика. Для звезд эти размеры до смешного малы. Поэтому,
чтобы увидеть перемещение звезд на фоне галактик, наблюдения производят
из разных точек земной